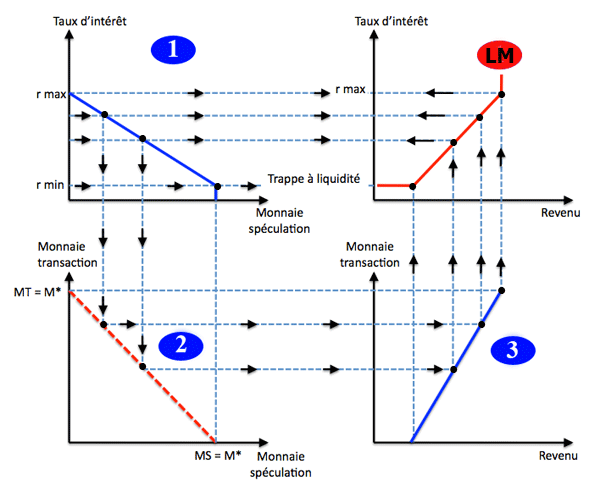
Le graphique n°1 décrit la liaison entre la demande de liquidités (demande de monnaie de spéculation) et le taux d'intérêt. Toutes choses égales par ailleurs, quand le taux d'intérêt augmente la demande de liquidités diminue. Lorsque le taux d'intérêt est très faible, la demande de liquidité est infinie (les placements n'ont aucun intérêt).
Le graphique n°2 applique la condition d'équilibre du marché de la monnaie : la demande de monnaie (pour les transactions et la spéculation) est égale à l'offre de monnaie M* qui est une donnée.
Le graphique n°3 reprend la liaison entre demande de monnaie de transaction et revenu : toutes choses égales par ailleurs, la demande de monnaie de transaction augmente quand le revenu augmente.
Le dernier graphique boucle le raisonnement : pour chaque taux d'intérêt il existe une valeur du revenu qui assure l'équilibre sur le marché de la monnaie.
Deux cas particulier sont généralement envisagés :
- Celui où la demande de monnaie pour réaliser les échanges est tellement importante (du fait de l’importance de Y) qu’elle absorbe toute la masse monétaire.
En supposant que L(Y,r) s’écrit L(Y,r) = LT(Y) + LS(r), ce cas signifie que LT(Y) = M*. Alors, LM est verticale (augmenter le taux d’intérêt n’a pas d’effet sur la demande de monnaie).
- Celui de la trappe à liquidité. Cas où les anticipations sont telles que la demande de monnaie est infinie, quel que soit le niveau du taux d’intérêt. Un taux d’intérêt plus bas n’a pas d’influence sur la demande de monnaie. LM est horizontale.
Cela revient à poser que la courbe LM est divisée en trois parties : la partie normale et les deux cas particuliers.