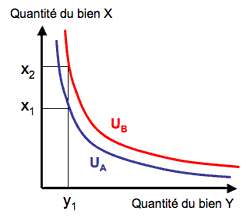
En présentant la théorie de l’utilité nous avons vu qu’on appelle utilité marginale d’un bien le supplément d’utilité procuré par la consommation d’une unité supplémentaire de ce bien (toutes choses égales par ailleurs - en particulier les quantités consommées des autres biens). Par définition, l’utilité marginale du bien X quand on passe de la quantité x1 à x2 est le rapport de l’augmentation de l’utilité procurée par ce changement de quantité (on passe de U1 à U2) à cette augmentation de quantité (on passe de x1 à x2). Mathématiquement l'utilité marginale est la dérivée première de la fonction d'utilité. L’utilité marginale du bien X quand on passe de x1 à x2 est le rapport de l’augmentation de l’utilité procurée par ce changement de quantité à cette augmentation de quantité. Soit (UB - UA) / (x2 - x1) En faisant varier x d’une très petite quantité le rapport précédent devient la dérivée première de la fonction d’utilité U’x= dU / dx Les courbes d’indifférence permettent de rendre compte visuellement de la manière dont s’opère la substitution entre les quantités des biens X et Y procurant une même utilité totale comme le montre ce graphique. Pour garder une utilité constante en consommant deux biens et en réduisant la quantité consommée de l'un des deux il faut consommer un peu plus de l'autre. 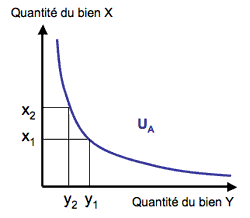Le taux marginal de substitution est le rapport des deux variation de l'utilité entraînées par le changement du panier. En consommant plus du premier bien, le consommateur augment son utilité totale, en consommant moins de l'autre il subit une perte d'utilité totale le taux marginal de substitution est donc normalement négatif. Sur ce graphique le passage de x1 à x2 jaisse l'utilité inchangée si dans le même temps on passe de y1 à y2. La fonction d'utilité pour ces deux biens s'écrit U = f(x,y). Le long d'une courbe d'indifférence, l'utilité totale ne varie pas ce qui signifie que la différentielle totale de la fonction U est nulle en cahcun des points de cette courbe. (δU/δx) dx + (δU/δy) dy = 0 Ce qui implique : dx / dy = - [(δU/δy) / (δU/δx)] Pour un point donné de la courbe d’indifférence le taux marginal de substitution est égal au rapport des utilités marginales des biens X et Y mesurées à ce point (au signe près).