Foyers
Soit une poutre continue à 5 travées, recevant un chargement sur la 4ème travée :
Effectuons une coupure sur l'appui A3 et gardons le tronçon de gauche.
Nous savons que le moment varie de façon linéaire dans les travées non chargées (chargement nul → effort tranchant constant → moment de flexion linéaire).
En admettant que le moment change de signe d'un appui à un autre (pour les zones non chargées), on observe que le moment passe par 0 sur la travée 3. Le point où le moment est nul se nomme "Foyer de la 3ème travée".
Imaginons que la force se déplace (en restant sur une travée supérieure à 3) :
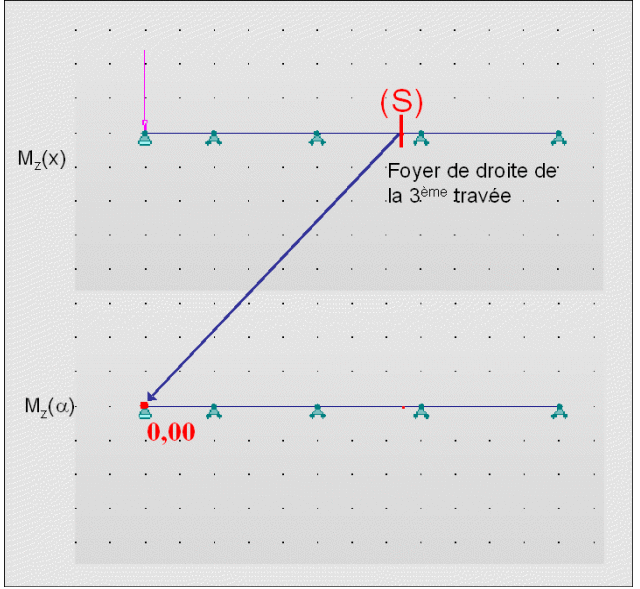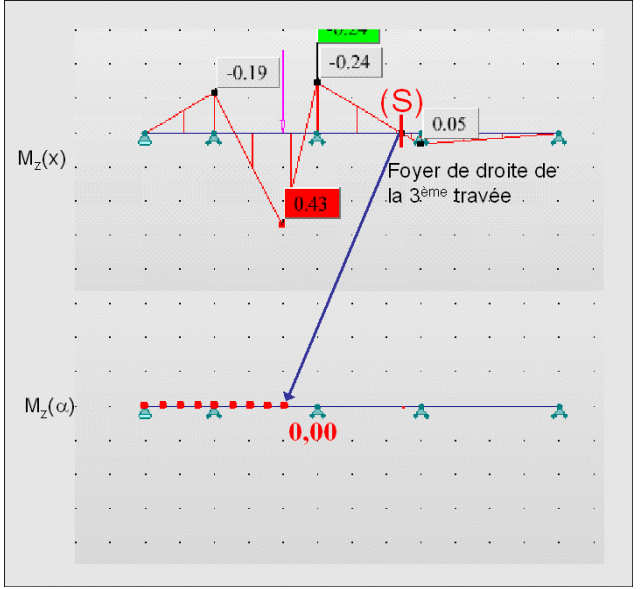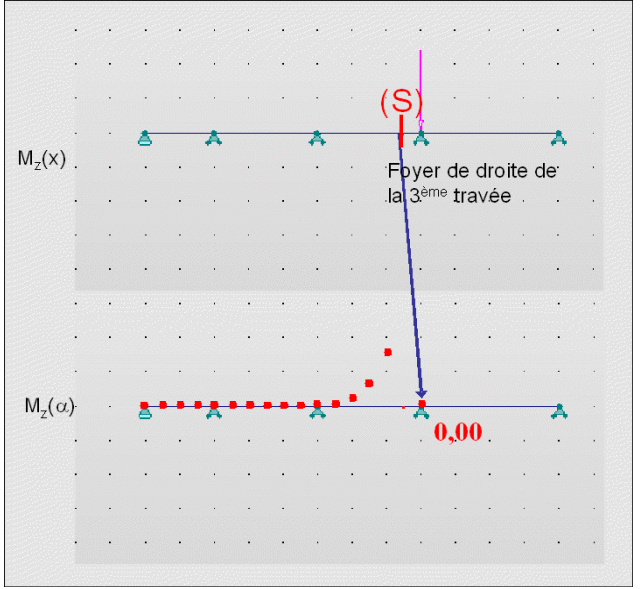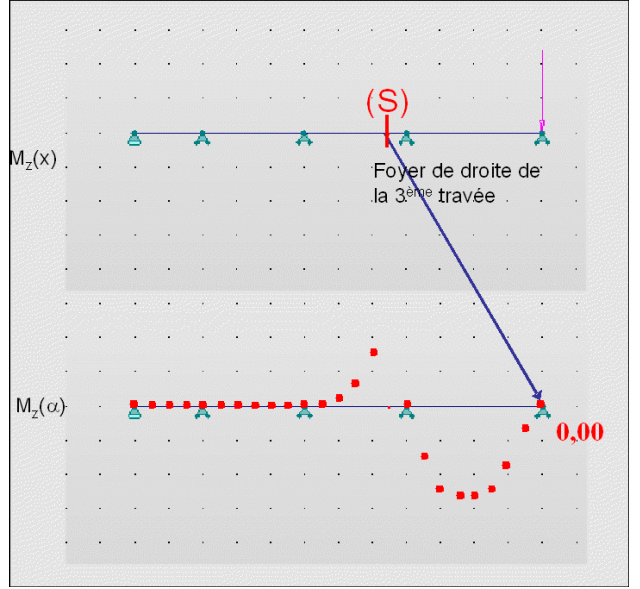
Le moment sur appui A3 change de valeur.
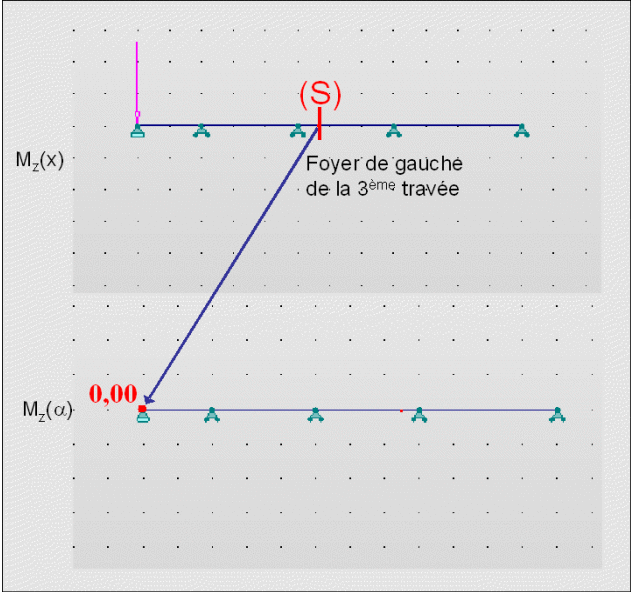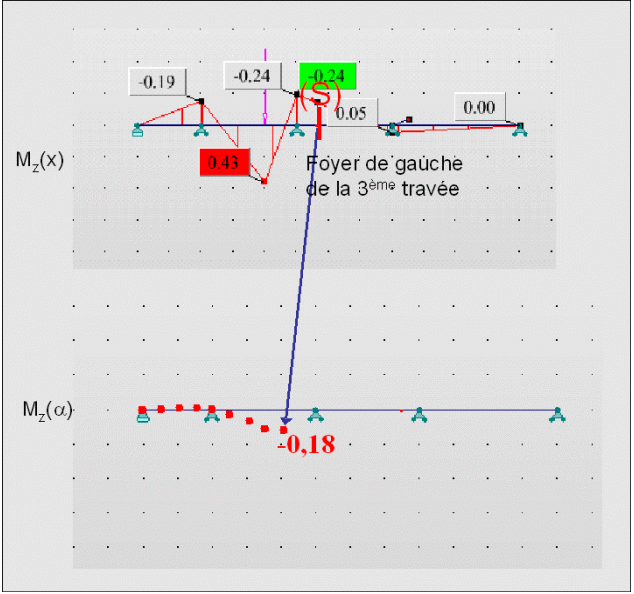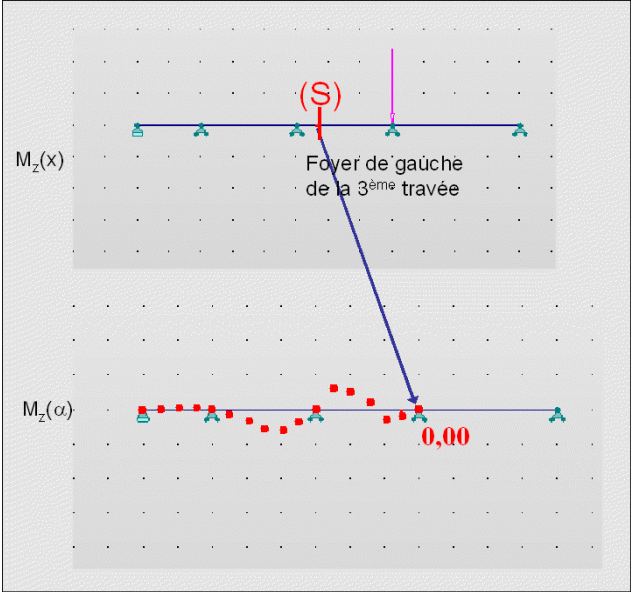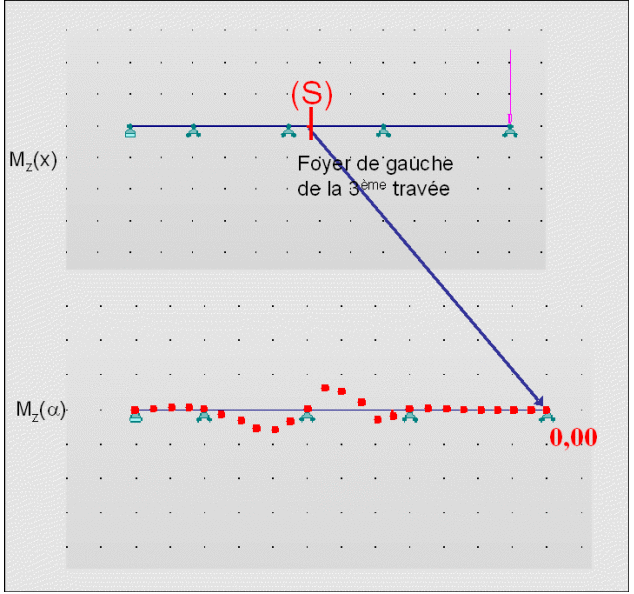
Posons α le facteur multiplicateur de ce moment. Tous les moments des 3 premières travées sont alors multipliés par α (proportionnalité au moment) :
On observe qu'au niveau du foyer de la 3ème travée, le moment reste nul.
Par conséquent, tant que la force est sur une travée supérieure à la travée i, le moment est nul au niveau du foyer gauche de la travée i.
Nous pouvons effectuer la même analyse pour un chargement qui serait placé avant la travée i. Dans ce cas, le moment resterait nul au niveau d'un point de la travée i (mais différent du foyer gauche). Ce point est appelé foyer droit de la travée i.
Dans chaque travée des poutres continues, il existe donc deux foyers.
Ces sections ont comme particularité d'avoir, comme ligne d'influence du moment de flexion, toute une partie nulle.
Le foyer gauche est celui où le moment est nul si le chargement est à droite de la travée possédant la section étudiée.
Le foyer droit est celui où le moment est nul si le chargement est à gauche de la travée possédant la section étudiée.
