MH :Equations différentielles homogènes

|
Défintion
Une équation différentielle homogène est une équation de la forme  qui reste inchangée
qui reste inchangée
quand on change  en en  et et  en en  tout en laissant tout en laissant  invariant invariant
La forme générale de ces équations est:
|
|
On pose  avec avec  fonction de fonction de 

On remplace dans l'équation différentielle et on obtient une équation différentielle de type
à variables séparables que l'on sait résoudre.
Les solutions sont sous forme paramétrique
|
|
|
Exemple corrigé:
Résoudre l'équation différentielle
|
|
|
Si on remplace  en en  et et  en en  tout en laissant invariant tout en laissant invariant  on obtient on obtient

L'équation est inchangée, c'est donc une équation homogène
|
|
On pose  avec avec  fonction de fonction de 

On obtient



La solution des l'équation est :
que l'on peut écrire aussi
|
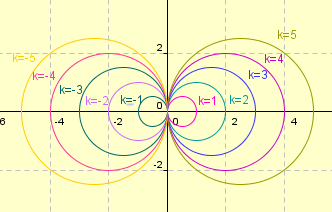
tracés des solutions de l'équation différentielle

pour k entier

|
Conditions initiales
|
|
Résoudre l'équation différentielle


la solution est le cercle

|
 |