Nous étudions dans ce chapitre une bobine à noyau magnétique : un circuit magnétique homogène porte un bobinage de n spires alimenté par une tension sinusoïdale de fréquence f.

1 Bobine idéale

Nous dirons que la bobine est idéale si les conditions suivantes sont réalisées:

è C1: la résistance du bobinage est nulle

è C2: les fuites magnétiques sont nulles

è C3: le circuit magnétique est linéaire, sans hystérésis ni pertes magnétiques.

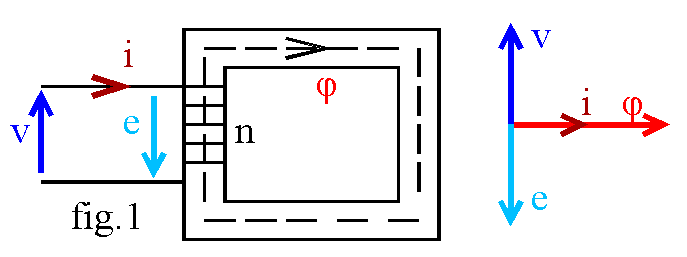
Étudions la bobine de la fig.1 alimentée par une tension sinusoïdale v = V.Ö2.sin(w.t)

L'intensité i est orientée par rapport à la tension v suivant la convention récepteur; le flux j dans le circuit magnétique est orienté à partir de i par la règle du tire-bouchon. La f.é.m. induite e, orientée dans le sens de i, est: e = -n.dj /dt, n étant le nombre de spires La loi des mailles donne v + e = 0 soit n.dj/dt = -e = v = V.Ö 2.sin(wt); nous en déduisons l'expression du flux: j = -(Ö2 /n.w).cos(wt). Le champ dans le circuit magnétique est b = j /S , S étant l'aire de la section droite du circuit magnétique; il vient: b = -B_m.cos(w.t) avec B_m = V.Ö2 /(n.w.S). Nous pouvons mettre cette relation sous la forme V = n.w.S.B_m/Ö2. En remplaçant la pulsation w par 2.p.f, il vient: V=(2.p/Ö2).n.S.f. B_m soit

V = 4,44.n.S.f.B_m

Cette relation, dite formule de Boucherot montre que le champ magnétique, donc le flux, est imposé pour une bobine donnée par la tension d'alimentation (V, f). Nous dirons que le flux est forcé par la tension.

En appliquant le théorème d'Ampère à la ligne de champ moyenne de longueur l il vient h.l = n.i .Le circuit magnétique étant linéaire, nous avons: b = µ.h avec une perméabilité absolue µ = Cste.

Il vient donc i = h.l / n = b.(l / µ.n) d'où: i = I_m.Ö2.coswt avec I_m= B_m.l / µ.n = V.Ö 2. l / (µ.n^².w S) .

L'inductance de la bobine est L = V.Ö2 / I_m.w = µ.n^².S / l .

Toutes les grandeurs étant sinusoïdales, nous pouvons les représenter sur le diagramme de Fresnel de la fig.1. Le déphasage y = (i ,v) = p / 2; la puissance active P consommée par le circuit est: P = V.I.cos y = 0; la puissance réactive est Q = V.I.sin y = V.I = L.w.I^².

Dans une bobine parfaite, alimentée par une tension v sinusoïdale, toutes les grandeurs sont sinusoïdales. Le flux est forcé par la tension suivant la loi de Boucherot :

V =4,44.n.S.f. Bmax

2 Influence de la résistance du bobinage

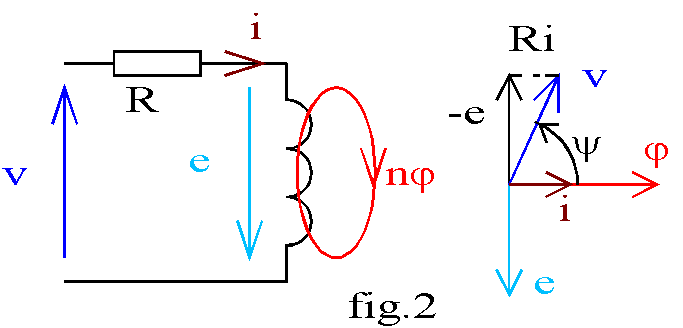
Nous reprenons la bobine étudiée au 1° et nous abandonnons la seule condition C1; soit R la résistance du bobinage; nous pouvons schématiser la bobine suivant le modèle de la fig.2.

Les équations de ce circuit sont: e = -n.dj / dt ; v = R.i - e ; j = b.S ; h = b / µ ; h.l = n.i.

Le circuit étant linéaire, la tension sinusoïdale v impose que toutes les grandeurs sont sinusoïdales. Prenons le flux j = F_m.coswt comme origine des phases. L'intensité est i = h.l / n = b.l /µ.n soit

i = j.l / µ.n.S ; elle est proportionnelle au flux donc est en phase avec le flux. La f.é.m induite

e = -n.dj / dt = n.w.F_m.sin wt est en quadrature arrière sur le flux; sa valeur efficace est :

E = n.w.F_m / Ö2= n.2.p.f..S.B_m / Ö2 soit E = 4,44.n.S.f.B_m; la loi de Boucherot lie maintenant le champ maximal à la f.é.m. efficace induite. Sur le diagramme de Fresnel de la fig.2, nous construisons la tension v = R.i - e.

Nous constatons que le déphasage y = ( i ,v) est inférieur à p / 2 et que la tension efficace est supérieure à E; la loi de Boucherot ne s'applique donc plus exactement; mais dans la plus part des cas (R.I)^² est très petit devant E^² donc V est peu différente de E et la loi de Boucherot peut être appliquée à la tension V avec une très bonne approximation.

La puissance active consommée est P = V.I.cos y = R.I^² = p_j = pertes par effet Joule de la bobine.

La puissance réactive consommée est Q = V.I.sin y = E.I.

Faisons une application numérique: le circuit magnétique de section S = 25 cm² de longueur l = 80 cm et de perméabilité relative µ_r =1 000, porte une bobine de n spires alimentée sous une tension sinusoïdale v de valeur efficace V = 220 V et de fréquence f =50 Hz.

è négligeons la résistance

Calculons le nombre de spires n pour avoir un champ maximal B_m = 1 T. La loi de Boucherot donne

n =V/( 4,44.S.f.B_m) = 396 spires.

L'excitation efficace est H= B / µ = B /µ_o.µ_r =(1/Ö2) / (4.p.10^-7 *10³) = 562,7 A.m^-1.

L'intensité efficace est I = H.l / n = 1,14 A.

La bobine absorbe les puissances active P = 0 et réactive Q = V.I = 250 vars.

è tenons compte de la résistance du bobinage R = 4 W

Nous pouvons calculer l'inductance de la bobine parfaite: j = b.S = µ.h.S = (µ.n.S / l).i ; le flux total à travers la bobine est n.j donc son inductance est L = n.j / i = µ.n^².S/ l soit L = 0,616 henry. Nous pouvons calculer l'impédance complexe Z = R + j.L.w de la bobine réelle soit

Z = (193,6 Ð 88,82°). Nous en déduisons l'intensité efficace I = V/ Z soit I = 1,14 A et le déphasage y = arg Z = 88,82°. Le flux efficace est F = L.I soit F = 1,77 mWb donnant un champ maximal B_m= FÖ 2 / S = 1,000 6 T.

Nous constatons que la résistance n'a quasiment pas modifié l'induction maximale.

La f.é.m efficace induite est E = L.w.I = 220,05 V quasi égale à V=220 V.

Les puissances consommées sont P= R.I^² = 5,2 W et Q =251 vars.

3 Influence des fuites magnétiques

Nous abandonnons les hypothèses C1 et C2 pour tenir compte de la résistance du bobinage et des fuites magnétiques.

Le flux total n.j_t dans la bobine se décompose en un flux n.j dans le circuit magnétique et en un flux de fuites n.j_f. Le coefficient d'Hopkinson n = j_t / j caractérise les fuites; nous avons

j_f = j_t - j = (n - 1).j.

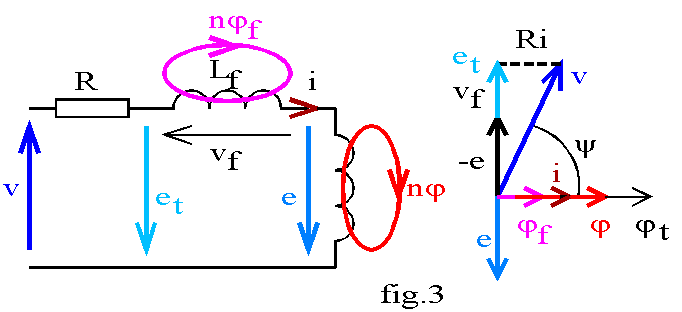
Nous avons vu (Cf. Chapitre 1.2) que les fuites pouvaient être modélisées par une inductance de fuites L_f ; le modèle équivalent de la bobine est alors représenté sur la fig.3. La f.é.m. induite dans la bobine parfaite est e = -n.dj/dt et celle induite dans la bobine réelle est

e_t = -n.djt /dt soit e_t = e + Lf .di /dt.

Les équations de ce circuit sont : e = -n.dj/ dt ; e_t = e - L_f. di /dt ; v = R.i

L'inductance de la bobine parfaite est L=n.j / i = µ.n^².S/ l l'inductance de fuites est

L_f =n.j_f / i =(n-1).L;

l'inductance de la bobine réelle est L_t = n.j_t / i = n.L.

La tension aux bornes de la bobine est v = R.i - e_t, déphasée de y par rapport à l'intensité.

La puissance active consommée est P = V.I.cos y = R.I^² = p_j.

La puissance réactive consommée est Q= V.I.sin y = L.w.I^² + L_f.w.I^²; elle est égale à la somme des puissances réactives nécessaires pour magnétiser le circuit magnétique et le circuit de fuites.

Reprenons la bobine étudiée dans l'exemple du paragraphe 2 et introduisons les fuites magnétiques avec un coefficient d'Hopkinson n =1,05.

L'inductance L a été calculée au paragraphe précédent: L = 0,616 H; l'inductance de fuites est donc

L_f = (n - 1).L = 31 mH. Nous en déduisons l'impédance complexe de la bobine réelle

Z=R + j.(L+L_f ).w = (203 Ð -88,87°). D'où I= V / Z = 1,08 A et y = 88,87°. Le flux efficace dans le circuit magnétique est F = L.I / n =1,68 mWb; le champ maximal dans le matériau magnétique est B_m= F.Ö2/S soit B_m = 0,952 T. Les fuites ont créé une diminution de ce champ de 5 % environ. Le flux efficace de fuites est F_f = L_f.I/n= 0,08 mWb. Les puissances consommées sont P = 4,7 W et Q = 238 vars; cette puissance se décompose en 227 vars pour le circuit magnétique et 11 vars pour le circuit de fuites.

L'introduction des défauts R et L_f modifie le flux dans le matériau magnétique pour une tension d'alimentation donnée; la plus part du temps, cette modification est négligeable (5% dans l'exemple).

Nous pourrons considérer que le flux est quasiment forcé par la tension suivant la loi de Boucherot.

4 Influence de la non linéarité du circuit magnétique

 

Nous négligeons la résistance et les fuites magnétiques (hypothèses C1 et C2) mais nous abandonnons C3: le circuit magnétique est non linéaire et présente une hystérésis magnétique. Le circuit magnétique est caractérisé par son cycle d'hystérésis représentant les variations du champ B dans la section droite en fonction de l'excitation H.

4.1 Courant magnétisant

Soit j = b.S le flux à travers la section droite du circuit magnétique; le théorème d'Ampère nous donne

i = H.l /n. Avec un changement d'échelles, la caractéristique magnétique b(h) représente j ( i ).

Soit v = -V.Ö2.sin(w.t) la tension d'alimentation; dans les hypothèses C1 et C2, comme au paragraphe 1, v = -e = - n.dj / dt; le flux est forcé par la tension et son expression est j = F_m.cos(w.t) avec

F_m = V.Ö2/n.w.

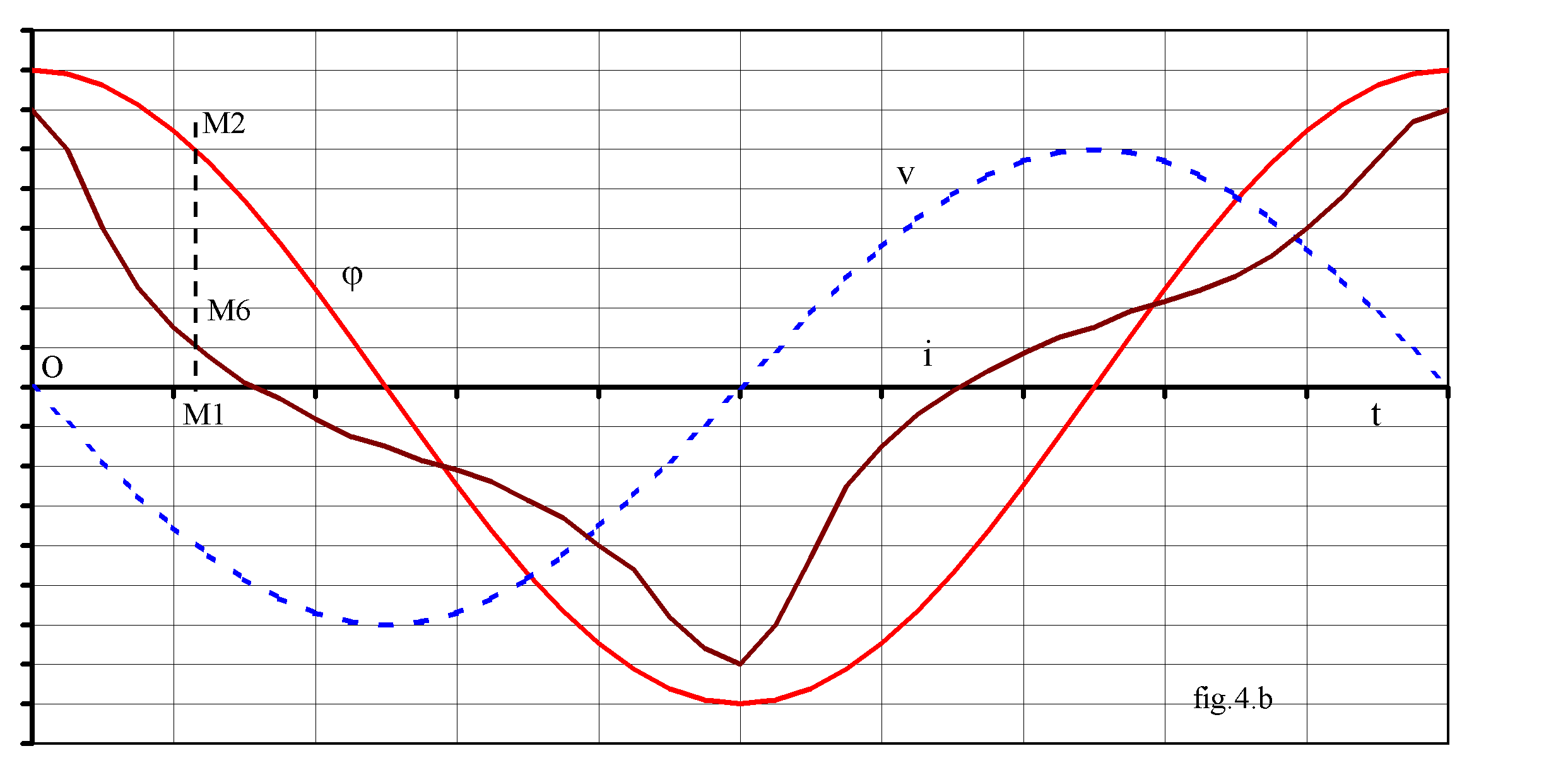
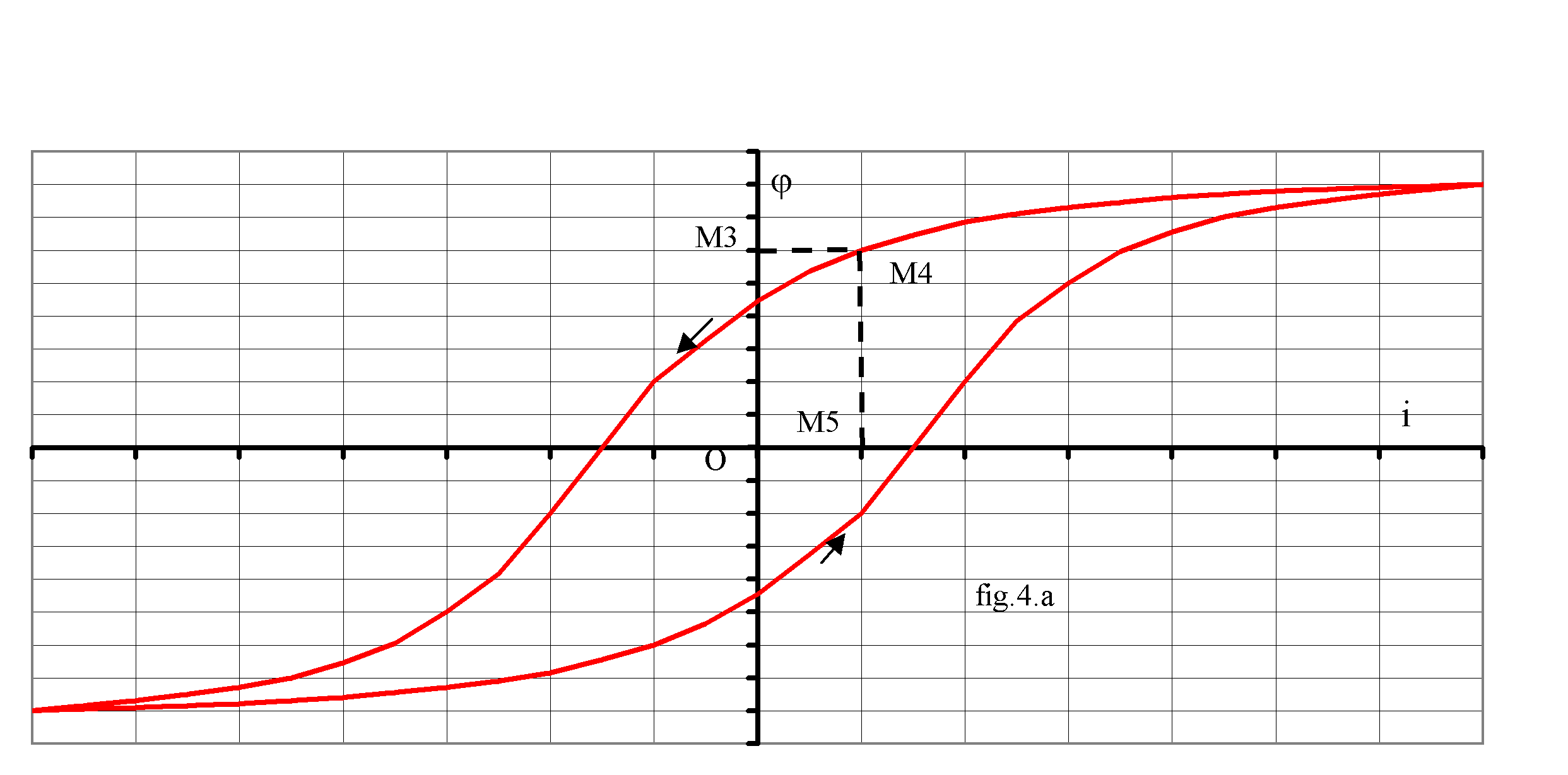
Représentons sur la fig.4.b les graphes de la tension et du flux en fonction du temps et sur la fig.4.a la caractéristique j ( i ) pour la même amplitude du flux

Pour une valeur du temps t correspondant à OM₁ sur la fig.4.b, nous déterminons la valeur du flux en M₁M₂. Nous reportons cette valeur en OM₃ sur le graphe j(i) en choisissant la branche du cycle d'hystérésis correspondant au sens de variation du flux ; à t choisi le flux décroît donc le point M₄ cherché est sur la branche supérieure; l'abscisse de ce point donne OM₅ représentant i (t); nous reportons cette grandeur en M₁M₆ pour avoir le graphe du courant. Nous construisons ainsi point par point une période du courant i (t)

La non linéarité du circuit magnétique crée une déformation du courant magnétisant i (t); l'intensité n'est plus sinusoïdale et a la même période T=1/f que le flux.

Cette intensité de fréquence f peut être décomposée en série de Fourier.; le graphe j(i) admettant l'origine O comme centre de symétrie, l'intensité est une fonction impaire et alternative; la série de Fourier n'aura donc que des termes en sinus de rang impair:

i (t) = I₁.Ö2.sin(w.t - y₁) + I₃.Ö2.sin(3.w.t - y₃) +I₅.Ö2.sin(5.w.t - y₅) + ... La valeur efficace de ce courant est : I =Ö[I₁^² +I₃^² + I₅^² + ... ]

La puissance active consommée par la bobine est égale aux pertes dans le fer p_f, somme des pertes par hystérésis et par courants de Foucault. Cette puissance est transmise par le seul fondamental du courant et vaut: P = V.I₁.cos y₁. La puissance apparente est S = V.I; la puissance réactive transmise par le seul fondamental est Q = V.I₁.sin y₁. La déformation du courant fait apparaître la puissance déformante : D = Ö [ S^² - P^² - Q^² ].

4.2 Modélisation de la bobine

L'apparition d'un courant non sinusoïdal dans la bobine complique beaucoup les calculs de circuit comportant de tels composants: nous ne pouvons plus utiliser les méthodes particulières au régime sinusoïdal (diagramme de Fresnel, valeurs complexes).

Pour pouvoir appliquer ces méthodes, nous allons substituer à la bobine réelle un modèle équivalent tel que, pour une même tension d'alimentation sinusoïdale:

è le champ créé par ce modèle soit égal au champ réel

è la puissance active consommée par le modèle soit égale à celle de la bobine réelle

è le courant magnétisant soit sinusoïdal.

La loi de Boucherot s'appliquant à la tension (R et L_f négligées), le champ magnétique maximal est donné par B_m = V/4,44.n.S.f; il ne dépend que du produit n.S caractéristique de la bobine; nous prendrons donc pour le modèle le même nombre de spires n et la même aire de section droite S.

Soit i'(t) =I'.Ö2.sin(w.t-y') le courant sinusoïdal du modèle équivalent, créé par la tension v(t)=V.Ö2.sinw.t. La puissance active consommée par le modèle est P'= V.I'.cosy'; elle doit être égale aux pertes dans le fer p_f = V.I₁.cos y₁, puissance transmise dans la bobine réelle par le fondamental du courant. Nous devons avoir: I'.cos y' = I₁.cos y₁.

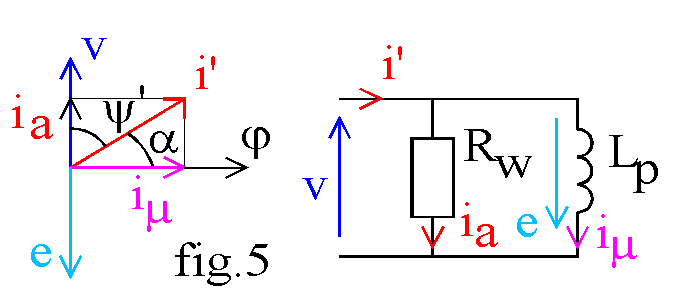
Pour le modèle, toutes les grandeurs étant sinusoïdales, nous pouvons les représenter sur un diagramme de Fresnel (fig.5). Nous représentons la tension v(t) et la f.é.m induite e = -v = - n.dj / dt; le flux est en quadrature avant sur la f.é.m: j = F_m.cosw.t; le courant est déphasé en arrière de

y' < p/2 sur la tension. Le flux n'est plus en phase avec le courant dans la bobine, l'angle a = (j , i') est appelé angle d'avance hystérétique; en réalité, la puissance perdue par pertes fer étant P= V.I'.sina , l'angle a est dû aux pertes par hystérésis mais aussi par courants de Foucault.

La caractéristique magnétique du modèle b(h) ou j(i' ) par changement d'échelles est alors la figure de Lissajous obtenue avec deux grandeurs sinusoïdales de même fréquence et déphasées de a: le cycle d'hystérésis du modèle est une ellipse.

La puissance réactive est Q = V.I₁.sin y₁; elle est véhiculée par le premier harmonique; cette puissance n'a aucune raison d'être égale à la puissance réactive Q =V.I'.sin y' correspondant au modèle. Cependant lorsque nous désirons prendre en compte les pertes par effet Joule de la bobine, et que nous voulons conserver l'égalité des puissances actives de la bobine réelle et du modèle, nous devons avoir les mêmes pertes par effet Joule dans le modèle et dans la bobine réelle; les valeurs efficaces des intensités I et I' doivent être égales. La condition

I'.cos y' = I₁.cos y₁ donne la valeur du déphasage : cos y' = (I₁ / I).cos y₁ .

Or I= I₁Ö [ 1 + I3^²/ I₁^² + I₅^²/ I₁^² +...], lorsque la saturation du circuit magnétique n'est pas très forte, l'amplitude des harmoniques du courant diminue rapidement lorsque leur rang augmente; nous pouvons confondre I et I₁ donc y' et y₁. Avec cette approximation, la puissance réactive réellement consommée par le circuit magnétique,

Q = V.I₁.cosy₁ , est peu différente de celle du modèle du circuit magnétisant Q' = V.I'.cosy'

Décomposons le courant i' en une composante active ia en phase avec la tension v et en une composante iµ en phase avec le flux.

Cette décomposition du courant nous amène à introduire le schéma équivalent du modèle représenté sur la fig.5.

Le courant actif passe dans une résistance R_w = V/I_a = V^²/p_f ; cette résistance modélise donc les pertes dans le fer du circuit magnétique. Le courant réactif i_µ passe dans une inductance L_p modélisant la création du flux dans le circuit magnétique; la composante i_µ est souvent appelée pour cela, composante magnétisante du courant. En toute rigueur cette inductance ne modélise pas la puissance réactive consommée par la bobine.

La bobine réelle n'étant pas linéaire, les composants R_w et L_p du schéma équivalent dépendent de la tension. Les pertes fer étant approximativement proportionnelles au carré du champ donc au carré de la tension, la résistance R_w = V^²/p_f est quasiment constante.

Les imperfections du circuit magnétique peuvent être modélisés en remplaçant la bobine réelle par un modèle équivalent parcouru par un courant sinusoïdal de même intensité efficace que le courant réel. Ce modèle admet pour schéma équivalent une résistance R_w modélisant les pertes dans le fer en parallèle avec une inductance L_p modélisant la création du flux; cette inductance ne modélise que de façon approchée la puissance réactive nécessaire pour magnétiser le circuit magnétique. Les éléments du schéma équivalent sont fonction de la tension appliquée.

 

5 Modélisation d'une bobine réelle

5.1 Schéma équivalent

Nous voulons modéliser la bobine réelle avec sa résistance, ses fuites magnétiques et son circuit magnétique non linéaire.

La puissance active consommée par la bobine réelle est P = V.I.cosy; elle est égale à la somme des pertes par effet Joule p_j = R.I^² et des pertes dans le fer p_f =R_w.I_a^².

La puissance réactive consommée est sensiblement égale à Q = V.I.siny; elle est la somme de la puissance réactive nécessaire pour magnétiser le matériau magnétique q_f = L_p.w.I_µ^² et de celle nécessaire pour magnétiser le circuit de fuites q_fui = L_f.w.I^² .

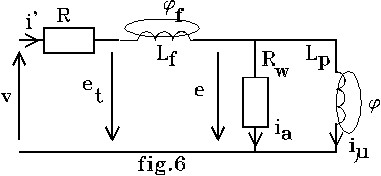
Si nous rassemblons tous les modèles obtenus, nous obtenons le modèle de la bobine réelle représenté sur la fig.6.

5.2 Mesure des éléments du schéma équivalent

La résistance R du bobinage se mesure avec un ohmmètre ou par une méthode voltampèremétrique en continu.

L'inductance de fuites L_f est la valeur la plus difficile à mesurer; nous pouvons bobiner n₁ spires sur le même circuit magnétique que la bobine étudiée et brancher un voltmètre de très grande impédance interne aux bornes de ces spires. Le flux j dans le circuit magnétique étant quasi sinusoïdal, la f.é.m induite dans les n₁ spires sera e₁= -n₁.dj /dt, de valeur efficace n₁.w.F. Nous en déduirons le flux utile efficace F.

Mesurons simultanément la tension efficace V, le courant efficace I'= I , avec un ampèremètre RMS pour tenir compte de la déformation du courant, la puissance active P consommée. De ces mesures nous pouvons déduire le déphasage y = (i',v) et donc calculer la f.é.m. complexe E_t = R I' - V et sa valeur efficace E_t; la f.é.m. et est créée par le flux total j_t dans les n spires de la bobine; nous en déduisons la valeur efficace de ce flux: F_t = E_t/n.w. Le flux j est en phase avec la composante magnétisante i_µ, le flux de fuites est en phase avec le courant i'; les deux flux sont donc déphasés; le flux de fuite étant faible devant le flux utile, nous pouvons négliger ce déphasage et dire qu'en valeurs efficaces F_f = F_t - F; nous en déduisons une valeur approximative de l'inductance de fuites:

L_f = n.F_f / I.

Des mesures précédentes, nous pouvons déduire:

è les pertes fer p_f = P - R.I^²

è la puissance réactive dans le fer: q_f = Q - L_f.w.I^²

è la puissance apparente S_f =.Ö ( p_f ^² + q_f ^² )

è la f.é.m efficace E=S_f / I

è R_w =E^² / p_f et L_p .w =E^² / q_f .

Nous avons alors tous les paramètres du schéma équivalent pour une tension d'essai V donnée.

5.3 Exemple

Soit une bobine de n =160 spires placées sur un circuit magnétique de section droite S = 30 cm^²; la résistance du bobinage est R = 4 W et l'inductance de fuites est L_f = 25 mH. Alimentée sous la tension sinusoïdale v de valeur efficace V= 127 V et de fréquence

f =50 Hz, elle est parcourue par un courant i d'intensité efficace I =1 A et consomme la puissance active P = 11 W.

Utilisons la méthode de Boucherot pour calculer les composants R_w et L_p du schéma équivalent; soit i' le courant sinusoïdal équivalent, le déphasage y = (i',v) est donné par cosy = P / V.I = 0,0866 d'où y = 85,03°; nous en déduisons la puissance réactive Q= P.tg y = 126,52 VAR.

La puissance fournie par - e_t est:

è puissance active P_t = P - R.I^² = 7 W

è puissance réactive Q_t = Q puisque R ne consomme pas de puissance réactive.

è puissance apparente S_t =Ö ( P_t^² + Q_t^² ) = 126,72 VA.

Nous en déduisons la valeur efficace de et : E_t = S_t / I = 126,72 V soit 0,23% de moins que V.

Nous pouvons en déduire la valeur efficace du flux total: e_t = -n.dj_t /dt donne :

F_t = E_t/ n.w = 2,521 mWb .

Le flux de fuite est F_f = L_f.I / n = 0,156 mWb.

De même la puissance fournie par -e est :

è puissance active P_f = P_t = 7 W car L_f ne consomme pas de puissance active

è puissance réactive Q_f = Q_t - L_f.w.I^² = 126,52 - 7,85 = 118,67 VAR

è puissance apparente S_f =Ö ( P_f^² + Q_f^² ) = 18,88 VA.

Nous en déduisons :

è la résistance R_w =E^² / P_f = 2 019 W.

è l'inductance L_p=E^² / Q_f .w = 0,379 H

è le courant actif I_a =P_f / E = 0,059 A

è le courant réactif I_µ = Q_f / E = 0,998 A

è le flux dans le circuit magnétique F = E / n.w =2,365 mWb

è le coefficient de fuites d'Hopkinson n = F_t / F =1,066

è l'angle de pertes magnétiques a = arc tg (I_a / I_µ) = 3,38 °

è l'induction efficace dans le fer: B = F / S = 0,788 T.

La formule de Boucherot appliquée à la tension V donnerait: B_m = V / (4,44.n.S..) =1,192 T soit

B = B_m / Ö2 = 0,843 T soit une erreur par rapport à la valeur exacte de 7 %. Compte tenu de la précision sur la valeur "exacte" de B obtenue à partir de plusieurs mesures et des hypothèses introduites dans la construction du modèle équivalent, nous pouvons considérer que la formule de Boucherot s'applique à la tension V avec une bonne approximation.