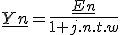Régimes transitoires : QCM
On étudie le réseau ci-dessous ; pour t = 0, K est ouvert et v = 5 V.
Pour t > 0, K est fermé.
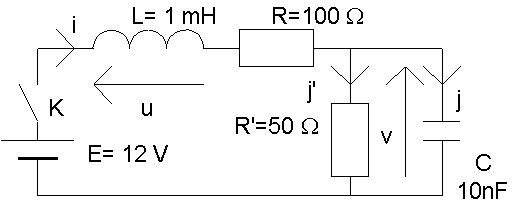
Question n°1 : u est une variable d'état
|
Oui
| |
|
Non
|
Question n°2 : At = 0+, i = 0
|
Oui
| |
|
Non
|
Question n°3 : At = 0+, j' vaut
|
- 100 mA
| |
|
0
| |
|
100 mA
|
Question n°4 : At = 0+, j vaut
|
- 100 mA
| |
|
0
| |
|
100 mA
|
Question n°5 : At = 0+, u vaut
|
0
| |
|
12 V
| |
|
17 V
|
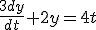
Question n°1 : la constante de temps est t =
|
3
| |
|
2
| |
|
1,5
|
Question n°2 : la solution particulière est y = 2t
|
Oui
| |
|
Non
|
Question n°3 : la solution de l'équation sans second membre est :
|
A.exp (- 1,5.t)
| |
|
A.exp 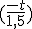
|
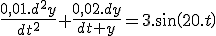
Question n°1 la pulsation propre est wo =
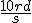
| |
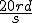
| |
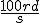
|
Question n°2 : le coefficient d'amortissement est z =
|
0,02
| |
|
0,1
| |
|
1
|
Question n°3 : la solution générale de l'équation sans second membre est y = A.exp(x.t) + B.exp(x'.t)
|
Oui
| |
|
Non
|
Question n°4 : y = 0,99.sin (20.t + 3) est solution particulière
|
Oui
| |
|
Non
|
Question n°5 : la solution générale de l'équation sans second membre oscille à la pulsation w =
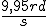
| |
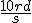
| |
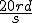
|
Soit le circuit d'équation 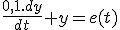 .
.
e(t) est périodique est de fréquence f = 10 Hz.
Question n°1 : si e(t) est en triangle, y(t) en régime permanent est un triangle
|
Oui
| |
|
Non
|
Question n°2 : si (e)t a une valeur moyenne 5, y(t) a pour valeur moyenne :
|
0
| |
|
5
| |
|
50
|
Question n°3 : si le fondamental de e(t) a une amplitude de 4, celui de y a une amplitude de :
|
0,6
| |
|
5
| |
|
40
|
Question n°4 : l'harmonique 3 de y est déphasé par rapport à l'harmonique 3 de :
|
- 87°
| |
|
0
| |
|
87°
|
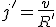 avec v = - 5V, j' = - 100 mA
avec v = - 5V, j' = - 100 mA
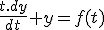
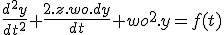
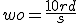
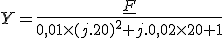
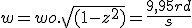
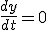
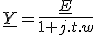 donc Y = 0,63
donc Y = 0,63