Dès 1941 aux États-Unis l’économiste russe Vassili Leontief analysa les liaisons techniques entre les produits et les consommations intermédiaires intervenant dans leur production.
Le tableau des entrées et des sorties TES est une présentation des équilibres emplois
ressources pour chaque produit.
Chaque ligne du produit permet de
retrouver cet équilibre. Le tableau a une dimension variable en
fonction du nombre de produits retenus.
Le TES est un tableau de synthèse des résultats. Mais c’est aussi un outil d’analyse dans la mesure où des liaisons stables peuvent exister entre les ressources et les emplois en produits.
Le lien est un coefficient technique de production.
Le coefficient technique de la branche i en produit j
(noté aij) est égal au rapport de la consommation intermédiaire du
produit j par la branche i (notée cij) à la production de la branche i
(notée pi) : soit aij = cij / pi .
Si on fait l’hypothèse (acceptable à
court terme) que les coefficients techniques sont constants, toute
modification de la valeur de la production entraîne un ajustement des
consommations intermédiaires, donc des productions des biens
correspondant et ainsi de suite....
Les coefficients sont calculés à partir d’un TES de
référence et peuvent être utilisés pour la prévision ou pour l’analyse
rétrospective. En matière de prévision, les spécialistes font des
hypothèses d’évolution des postes d’emploi final, la consommation
finale, la FBCF, les exportations, les variations de stocks. Ils
peuvent alors observer les modifications engendrées dans le TES par les
variations initiales de production permettant de répondre à ces
hypothèses d’évolution de la demande.
Le TES est devenu un outil indispensable aussi bien pour la prévision que pour la simulation, donc pour la politique économique.
À titre d’exemple le tableau suivant est construit pour quatre branches ce qui donne quand même plus de 90 cases (contre 3192 dans la version des comptes nationaux).
Les produits sont les suivants :
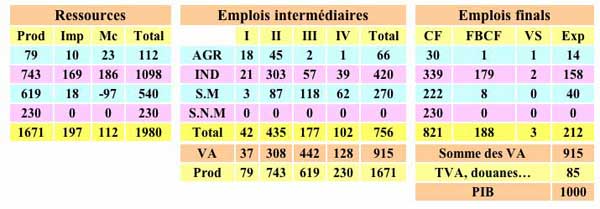
On peut facilement construire la matrice des coefficients techniques à partir du tableau des emplois intermédiaires. Par exemple le coefficient technique de l'agriculture en produits de l'industrie est le rapport 21 / 79. La consommation intermédiaire de produits industriels par l'agriculture vaut 21 et la production totale de l'agriculure vaut 79, autrement dit pour produire une valeur de 79 en produits agricoles, il faut utiliser une valeur de 21 en produits industriels.
Si on numérote de 1 à 4 les branches, on voit que :
P1 + M1 + Mc1 = a11 P1 + a12 P2 + a13 P3 + a14 P4 + CF1 + FBCF1 + VS1 + X1
P2 + M2 + Mc2 = a21 P1 + a22 P2 + a23 P3 + a24 P4 + CF2 + FBCF2 + VS2 + X2
P3 + M3 + Mc3 = a31 P1 + a32 P2 + a33 P3 + a34 P4 + CF3 + FBCF3 + VS3 + X3
P4 + M4 + Mc4 = a41 P1 + a42 P2 + a43 P3 + a44 P4 + CF4 + FBCF4 + VS4 + X4
En faisant, à partir d'enquêtes, des hypothèses sur l'évolution de la consommation, de la FBCF, des comportements de stocks et des importations et exportations le système de 4 équations ne comporte plus que 4 inconnues : les productions P1, P2, P3, P4.
Le système a une solution facile à calculer. On sait ainsi chiffrer les conséquences sur l'ensemble de l'économie d'une modification d'un poste quelconque de la demande d'un produit.